Tanner's Website

After learning about Smith numbers today I cooked up this script fairly quickly. There are many places where it could be optimized and cleaned up but that wasn’t really the point – I just needed something that was accurate, and I’m pretty sure this is.

It also helped me to learn about the ulimit command after running it with a HUGE number that had taken up about 7GB of swap before I had to kill the process remotely via SSH…

#!/usr/bin/python
# smith number detector - TWS 1-12-13

def detectSmith(num):
  if(sumFactors(num) == sumDigits(num)):
    return True
  else:
    return False

# calculate the sum of the factors
def sumFactors(num):
  factorList = factors(num)
  sum = 0

  for factor in factorList:
    if factor > 9:
      # if a number (base ten) has multiple digits it has to be broken down
      sum = sum + sumDigits(factor)
    else:
      sum = sum + factor

  return sum

# sum the digits in a number with two or more
def sumDigits(num):
  sum = 0  

  if num > 9:
    while num > 9:
      sum = sum + num % 10
      num = num / 10
    sum = sum + num
    return sum
  else:
    # should never reach this
    return num

def factors(num):
  primeFactorList = []

  factor = lowestPrimeFactor(num)
  currentNum = num

  while factor != -1:
    primeFactorList.append(factor)
    currentNum = currentNum / factor
    factor = lowestPrimeFactor(currentNum)

  if(currentNum != num):
    # preventing returning the number passed in
    primeFactorList.append(currentNum)

  return primeFactorList

def lowestPrimeFactor(num):
  for x in range(2, (num / 2) + 1):
    if(num % x == 0):
      return x
  return -1

for number in range(1, 1000):
  if(detectSmith(number)):
    print "The number", number, "is a Smith number."

A simple script I use for work to search the contents of files. It just wraps up ‘find’ and ‘grep’ to recursively search and display the location of the file.

#!/bin/bash
# Tanner Stokes - 8-23-12
# Search contents of files

if [ -z "$1" ] || [ -z "$2" ]
then
echo "Usage: csearch \"filetype\" \"content\""
echo "ex: csearch \"*.php\" \"my_function()\""
exit 1
fi

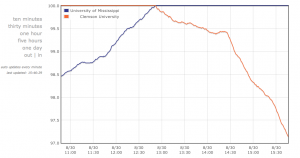
find . -name "$1" -exec grep -Hn "$2" {} \;